Hi intrepid readers, so here’s me homeworking again.

First, the classroom action:

My first week of semester 2 classes has been pretty great. Both math classes have had a full 5 days of beginner-Thinking-Classroom stuff: verbally delivered problems that have interesting patterns / solutions, room for extensions, and working in visibly random groups on whiteboards & windows.

There’s been majority buy-in from the students so far, and the rest are pretty firmly in the “I hate math class because math class has always hated me” camp from what I can tell. No one’s had a meltdown over not working with their favorite friends. I have had a few questions along the lines of, “So when are we going to have a normal class?”, but I’ve just kind of shrugged that off. “Maybe never, we’ll see!”

Content-wise, it’s all been a selection of Good Problems taken from either what I’ve worked on in class myself or from Peter’s site. I’ve been using the same ones in both my Foundations 11 and my Math 10 classes … which just backfired today as the afternoon grade 10 class had talked with someone from the morning 11 class and been given “the answer”. (They still didn’t know *why* it was the answer and they kind of spilled the beans in asking me, but it did mean the time spent on the problem was significantly shorter.) Oh well, was going to move to curriculum-specific problems tomorrow anyway!

I have a few coursework-specific questions to answer that I’ll put after the break.

Comment on how the power curve (hockey stick) plays a role in your classroom.

Okay, so here’s the idea: we often mistake our classrooms as being on a normal curve in all respects. We observe specific behavior that catches our attention, and we default to thinking that this is probably representative of, if not a majority, then at least some notable part of a lump centered around a nearby average.

But what if the behavior that most catches our attention isn’t part of a normal curve, but on a power law?

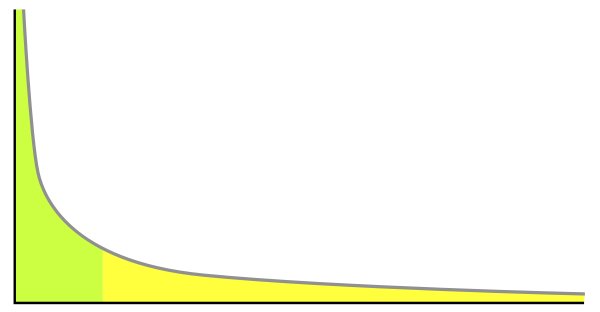
Those disengaged, complaining folks? Outliers. Alternately, those super-keen, hands-up, always excited for more? Sadly, probably also outliers. But once we think in these terms, we can remember to look around at the other 80% of the room and see how they’re doing. If we’ve got something going good for them, then probably we’re doing all right (and maybe we’ll even have time to spend a ton of energy on the other 20%, maybe).

This isn’t prescriptive – it doesn’t say whether you should spend most of your time on the outliers or not. Sometimes you can afford to, and need to; sometimes you need to balance out the demands from the end of the hockey stick with the needs of the other 80%. But in either case, a more realistic perspective on your whole class can only be a good thing.

Comment on the Van De Walle reading. In particular respond to the quote on the front page by Schifter and Fosnot vis-à-vis the reading.

“…they cannot understand for their students…”

Yep. No amount of me understanding is going to magically download to my students.

What my understanding can help with, however, is as a guide to what sorts of useful questions to ask. If I want students to see how a concept fits together, I can pose problems to them in which the concept is a good fit; I can ask them questions that help them see misconceptions for what they are; I can suggest models which might be a useful approach on their way to understanding.

Having read the Van De Walle article, respond again to – what does it mean to learn mathematics?

To learn mathematics is to do the mental work of finding and working out new mathematical concepts, as well as (in some cases) to learn / create procedures and strategies for doing useful things with those concepts. (“Useful” being entirely flexible and not restricted to actually-pragmatic-in-real-life things.)

Last week we discussed the studenting data. Studenting is a proxy for learning in that it is what happens in a classroom in place of learning. Are there any proxies for learning in your teaching practice?

Perhaps. I don’t think I have a good answer for this yet; maybe the times when I ask students to definitely write something down in particular, even though I really just want to know they’re engaging with the material enough to write something down.

Comment on your experiences with giving problems verbally. What are you noticing about yourself? Your students?

I’m noticing that there’s a lot less downtime, and in a sense a lot less prep time – I don’t have to type this up myself, or create a worksheet out of it and get it photocopied, I just have to know the problem well enough to describe it. Students will ask questions pretty quickly when they haven’t understood the problem – much better than them waiting, or staring at a page, and easily answered for the most part.

I have noticed that if I mis-word something the first time, it’s pretty likely that someone will miss the correction! Even if clarification and detail are expected, it’s good to at least state the basic problem concisely and clearly.

I have some more responses to add for Week 4’s journaling (much of the above is catching up for week’s 2 and 3), but since they’re primarily on meaningful notes, which I’m just barely starting on w/ this semester’s classes, I’ll add more on that later.